Maxwell 方程式
真空中に電荷と電流が存在し、分極と磁化がない場合、電磁場を表すMaxwell 方程式は、CGS-Gauss 単位系を用いると次のように書ける。
(1) ![]()
(2) ![]()
(3) 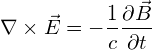
(4) 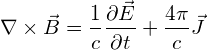
スカラーポテンシャル ![]() 、ベクトルポテンシャル
、ベクトルポテンシャル ![]() を用いて
を用いて![]() と
と![]() を表す。(J.D. Jackson 6.4 参照)
を表す。(J.D. Jackson 6.4 参照)
(5) 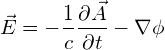
(6) ![]()
さらに、ローレンツゲージをとると、Maxwell方程式 (1)-(4)は、以下の2つの2階偏微分方程式になる(J.D. Jackson 6.5 参照)。
(7) 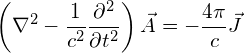
(8) 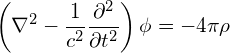
式(7)は、電流(電子ビーム)が作る電磁波を表す波動方程式であり、FELの増幅作用を解析するのに必要な式である。式(8)は、空間電荷による静電波を表す式で、FEL(Compton 領域)の議論では無視できる。
