Dicke のSuperradiance -3

投稿日: 2015年11月7日作成者: rh

前回までに、２つのエネルギー準位をもつ２個の原子が共鳴的に結合した系において、系の取りうるエネルギー準位とその遷移確率を求めた。この遷移確率を用いて、完全反転分布（２個の原子ともに上準位にある）からの光子の放出確率を時間の関数として求めてみよう。

この系は３つのエネルギー準位（４つの状態）を持つ。時刻 $t=0$ において２個の原子ともに上準位にある時、 $t>0$ における各準位の存在確率は以下の微分方程式に従う。下付き添え字の $ee$ は二つの原子がともに上準位、 $gg$ はともに下準位、 $s$ と $a$ は上準位と下準位の組み合わせで波動関数が対称、反対称の場合である。

$\displaystyle \frac{dP_{ee} (t)}{dt}= -2\gamma P_{ee}(t)$

$\displaystyle \frac{dP_s (t)}{dt}= 2\gamma P_{ee}(t) - 2 \gamma P_s(t)$

$\displaystyle \frac{dP_a (t)}{dt}=0$

$\displaystyle \frac{dP_{gg} (t)}{dt}=2\gamma P_s(t)$

これを解いて、

$\displaystyle P_{ee} (t) = \exp (-2\gamma t)$

$\displaystyle P_s (t) = 2 \gamma t \exp (-2\gamma t)$

$\displaystyle P_a (t) = 0$

$\displaystyle P_{gg} (t) = 1 - (1+2 \gamma t) \exp (-2\gamma t)$

となる。光子の放出確率は

$\displaystyle W_2 (t) = \gamma_{ee,s} P_{ee} + \gamma_{s,gg}P_s = 2 \gamma (1+2\gamma t) \exp (-2 \gamma t)$

である。

ところで、原子が１個の場合、原子が上準位に存在する確率 $P_e(t)$ は次式に従う。

$\displaystyle \frac{dP_e (t)}{dt}=-\gamma P_e(t)$

これを解くと

$\displaystyle P_e (t) = \exp (-\gamma t)$

となり、上準位の存在確率は指数的に減少する。このときの時定数（寿命）が $1/\gamma$ である。準位間の遷移にともなう光子の放出確率は

$\displaystyle W_1(t) = \gamma \exp (-\gamma t)$

である。

２個の原子が独立に存在する場合と共鳴的に結合する場合の光子の放出確率の比は

$\displaystyle \frac{W_2(t)}{2W_1(t)}= (1+2\gamma t)\exp (-\gamma t)$

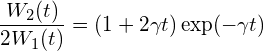
となる。

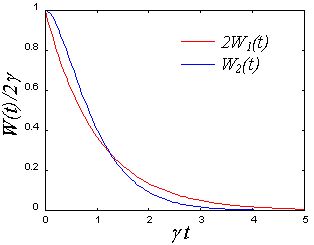
２つの場合について光子の放出確率を図示すると以下のようになる。２個の原子が共鳴的に結合することで、光の放出確率は指数的な減衰とは異なる曲線を示す。共鳴的に結合する原子の数が増えるとこの相違はさらに顕著になる。

カテゴリー: レーザーパーマリンク

コメントを残すコメントをキャンセル