いよいよ完全反転分布したN個の2準位原子からなる系からの光放出の時間波形の計算を行う。
下図のようにエネルギー準位のラベルづけを行う。
準位![]() から
から![]() への遷移確率は、前回までに求めた式を
への遷移確率は、前回までに求めた式を ![]() で書き直して
で書き直して
![]()
である。
時刻![]() に準位
に準位![]() に系の状態を見出す確率は次の微分方程式に従うことがわかる。
に系の状態を見出す確率は次の微分方程式に従うことがわかる。
![]()
完全反転分布の初期値 ![]() ,
, ![]() について、この微分方程式を解けば光放出の時間波形を求められる。しかしながら、
について、この微分方程式を解けば光放出の時間波形を求められる。しかしながら、![]() に対して計算するのは煩雑である。ここでは別の方法で近似計算を行う。
に対して計算するのは煩雑である。ここでは別の方法で近似計算を行う。
完全反転分布した状態から ![]() 個の光子を放出する平均時間を
個の光子を放出する平均時間を![]() と表すことにする。各準位間の遷移の平均時間を足し合わせれば任意の
と表すことにする。各準位間の遷移の平均時間を足し合わせれば任意の ![]() について
について ![]() を計算できて、
を計算できて、
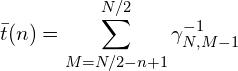
![Rendered by QuickLaTeX.com \displaystyle = \gamma^{-1} \sum_{M=N/2-n+1}^{N/2} \left [(N/2+M)(N/2-M+1) \right ]^{-1}](https://e-beam.sakura.ne.jp/physics/wp-content/ql-cache/quicklatex.com-a718435ef29ab618dfb44c6908e34477_l3.png)
![]() の場合、和を積分に置き換えて近似計算ができるので、
の場合、和を積分に置き換えて近似計算ができるので、
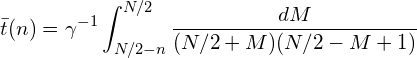
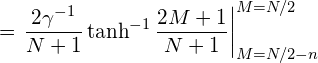
これを ![]() について解くと
について解くと
![]()
![]()
が得られる。光放出の時間波形は
![]()
と求められた。

