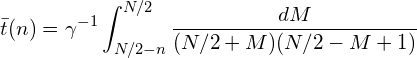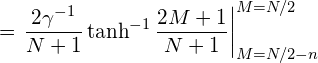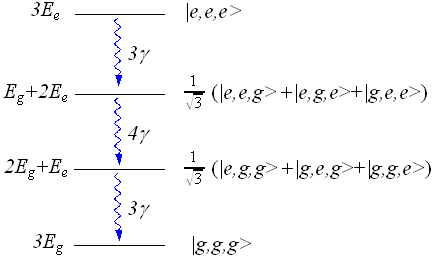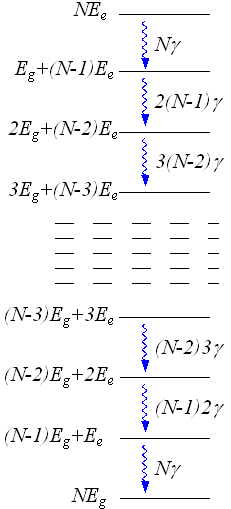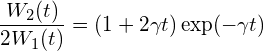前回の記事を公開した後、「遷移双極子モーメントとは何か」や「遷移確率が遷移双極子モーメントの二乗に比例する理由は」といった解説も必要ではないかと考えた。しかし、これらの質問に対する回答は容易に入手できる教科書やインターネット上の情報で補えるので、ここでは深入りしないことにする。(時間があれば、このあたりの話もまとめたいが、いつの日になるか、、、)
本題を進める。
前回は、2つのエネルギー準位を持つ原子において、光の放射を伴う準位間の遷移を取り上げた。次に、このような原子2個からなる系で生じる「共鳴的に強く結合した状態」を導く。
2個の原子の間隔は光の波長に比べて十分小さいとし、光の電場は位置によらず一定と考える。
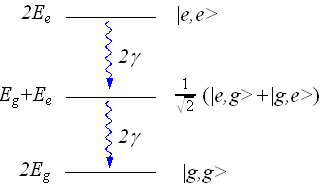
このような系が取りうるエネルギー準位は 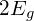 ,
, 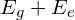 ,
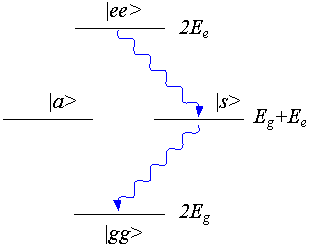
, 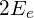 の3通りである。2番目のエネルギーは、対称と反対称の2つの状態に分けられるので、4通りの状態がありうる。
の3通りである。2番目のエネルギーは、対称と反対称の2つの状態に分けられるので、4通りの状態がありうる。
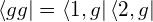
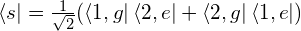
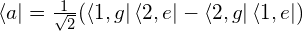
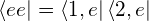
ここで、1, 2 は原子のラベルである。
全双極子モーメント 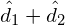 を介して起こりうる遷移確率は、
を介して起こりうる遷移確率は、
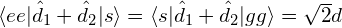
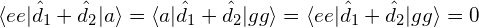
と求められる。つまり、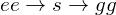 の遷移は許容されるが、
の遷移は許容されるが、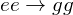 および
および 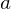 を通る遷移は許されない。
を通る遷移は許されない。
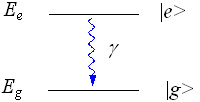
許される遷移と許されない遷移があるのは、始状態と終状態のパリティ(電子の状態間数が奇関数か偶関数か)による。1個の光子を放出・吸収するような遷移はパリティの異なる状態間のみで許される。
図に示すと以下のようになる。
遷移確率が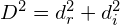 に比例することから、原子が1個の時の遷移確率を
に比例することから、原子が1個の時の遷移確率を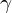 とすると、原子が2個の場合は
とすると、原子が2個の場合は
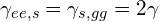
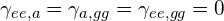
となる。
2個の原子が近接して存在する場合、原子が独立に存在する時とは異なる様相を示すことがわかる。これが「複数の原子が系の内部で放出された放射場によって互いに共鳴的に強く結合した状態」である。
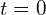 における光強度は、N個の独立した原子からの自発放射の和に等しく、
における光強度は、N個の独立した原子からの自発放射の和に等しく、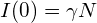 である。
である。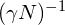 であり、原子数に反比例して狭くなる。
であり、原子数に反比例して狭くなる。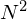 に比例する。
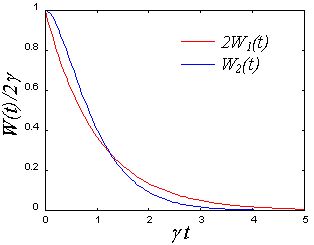
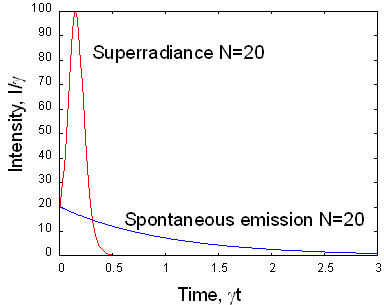
に比例する。![]() の場合の時間波形を図示する。
の場合の時間波形を図示する。![]() で規格化している。
で規格化している。

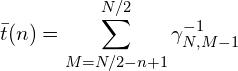
![Rendered by QuickLaTeX.com \displaystyle = \gamma^{-1} \sum_{M=N/2-n+1}^{N/2} \left [(N/2+M)(N/2-M+1) \right ]^{-1}](https://e-beam.sakura.ne.jp/physics/wp-content/ql-cache/quicklatex.com-a718435ef29ab618dfb44c6908e34477_l3.png)